Jennifer Sertl posted a link to a post by Pete Flint, General Partner at NFX
The post explores the constraints on building and scaling two sided marketplaces
I'll use it as an excuse to revisit some old ideas about the long tail economics of digital marketplaces
Let's begin by observing both the supply and the demand side of any digital marketplace is subject to long tail economics
Or, what is more popularly called the 80/20 rule
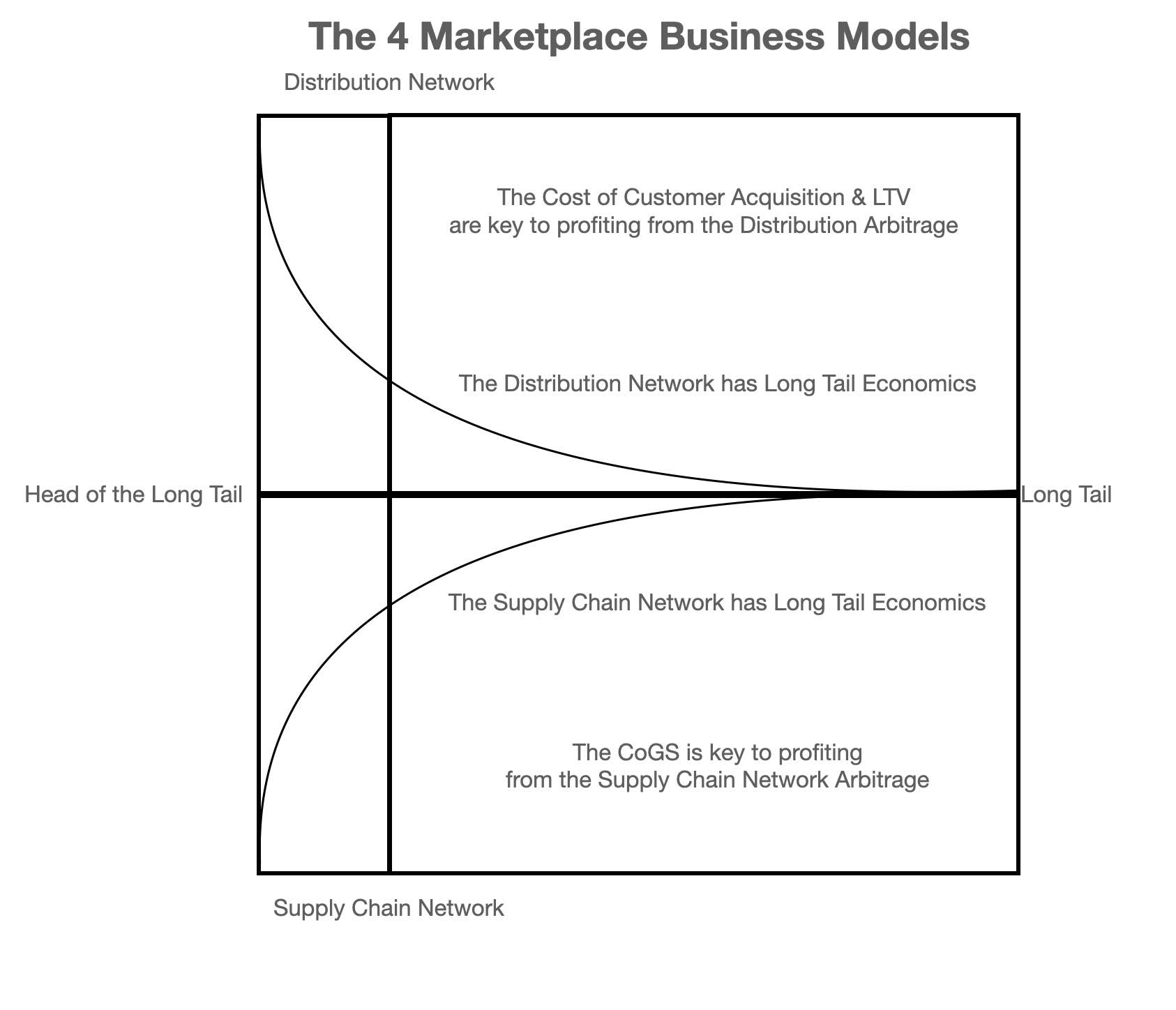
This suggests there are four key models you can adopt when building a marketplace
But before we take a look at those models let's first observe that the supply and demand sides of the equation are basically an arbitrage play
The demand side is a game of margins around cost of customer acquisition
The supply side is a game of margins around the cost of goods and services
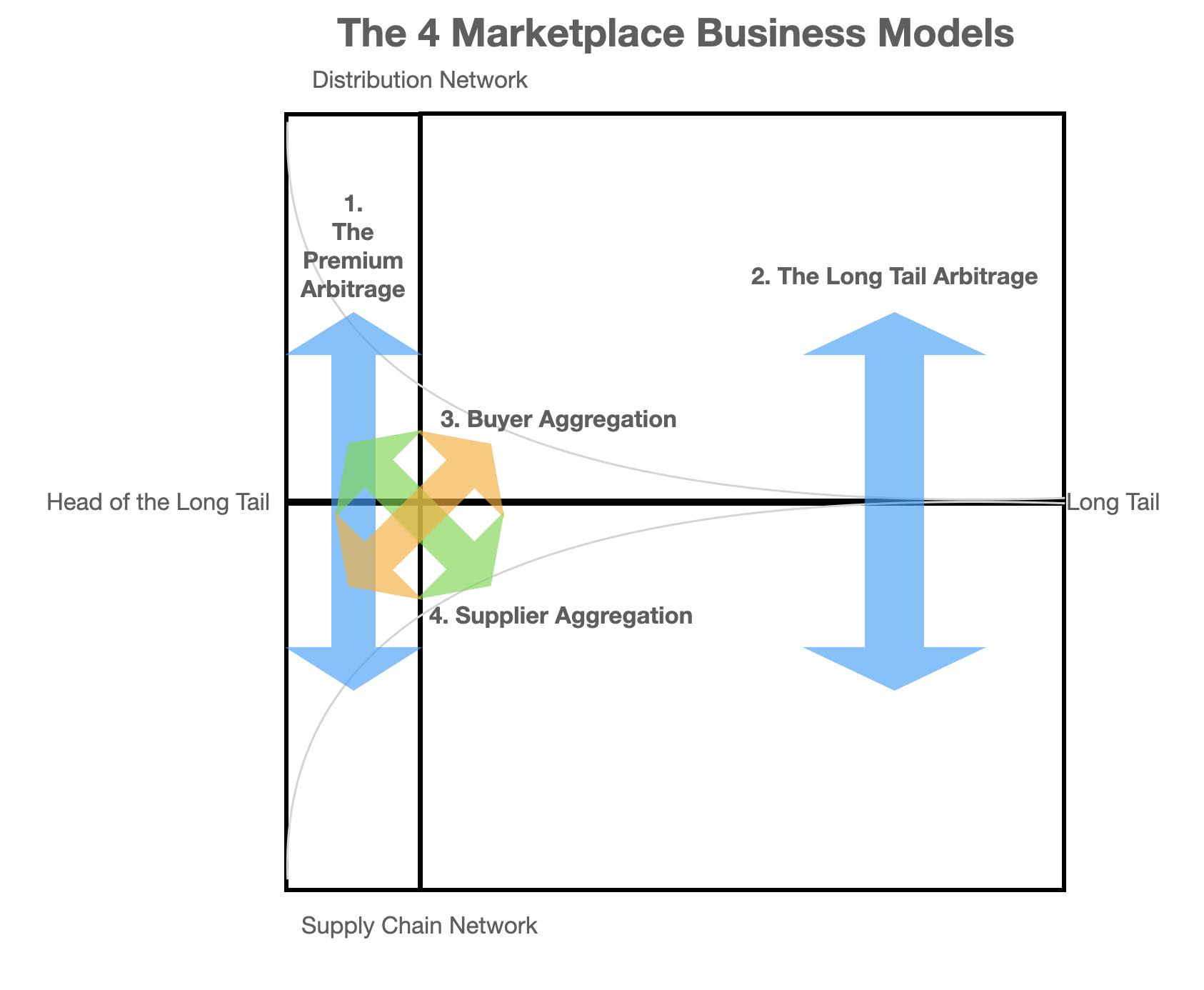
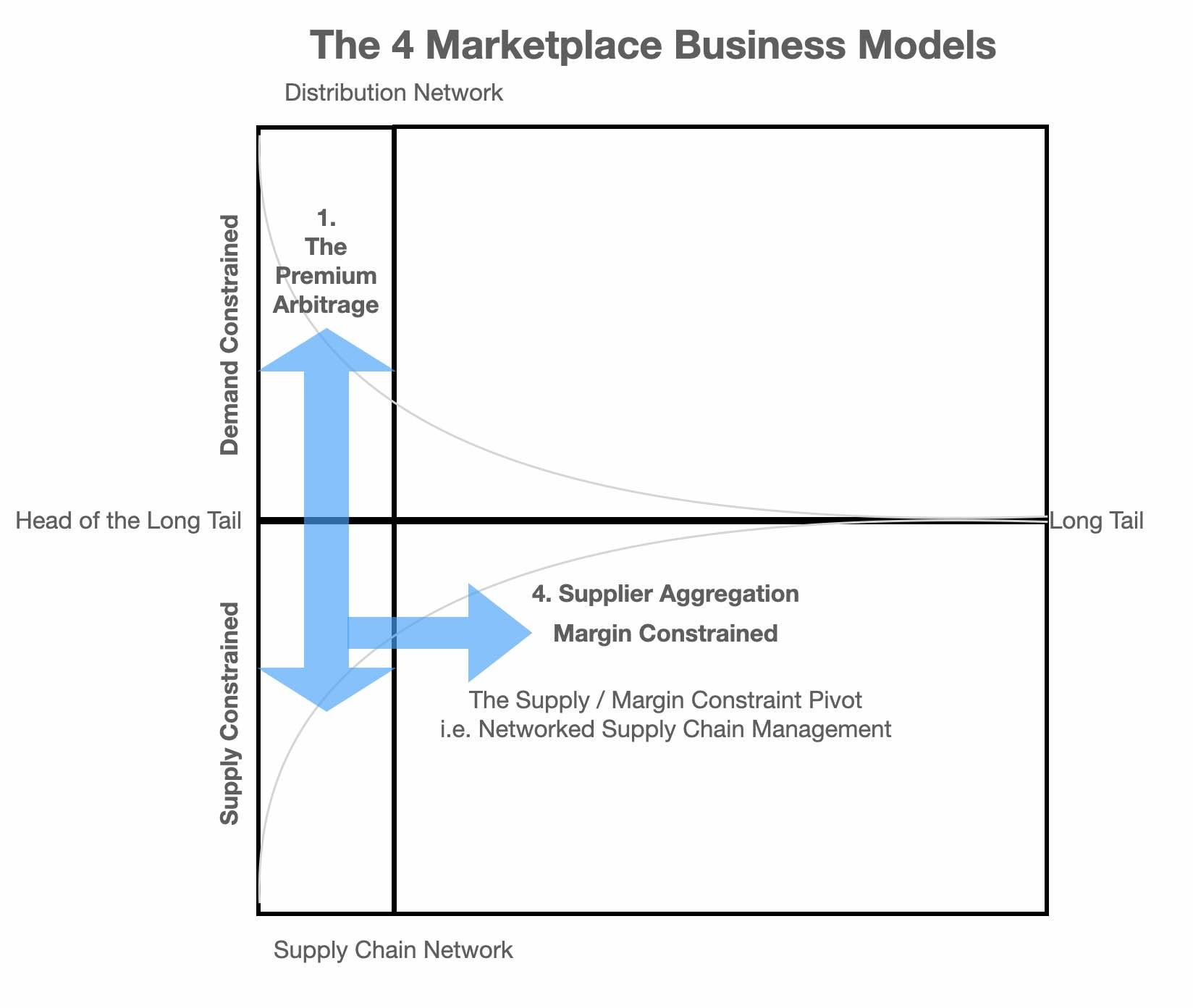
If we map this observation across the 4 quadrants we discover the constraints of servicing each quadrant
Now let's look at the 4 key business models
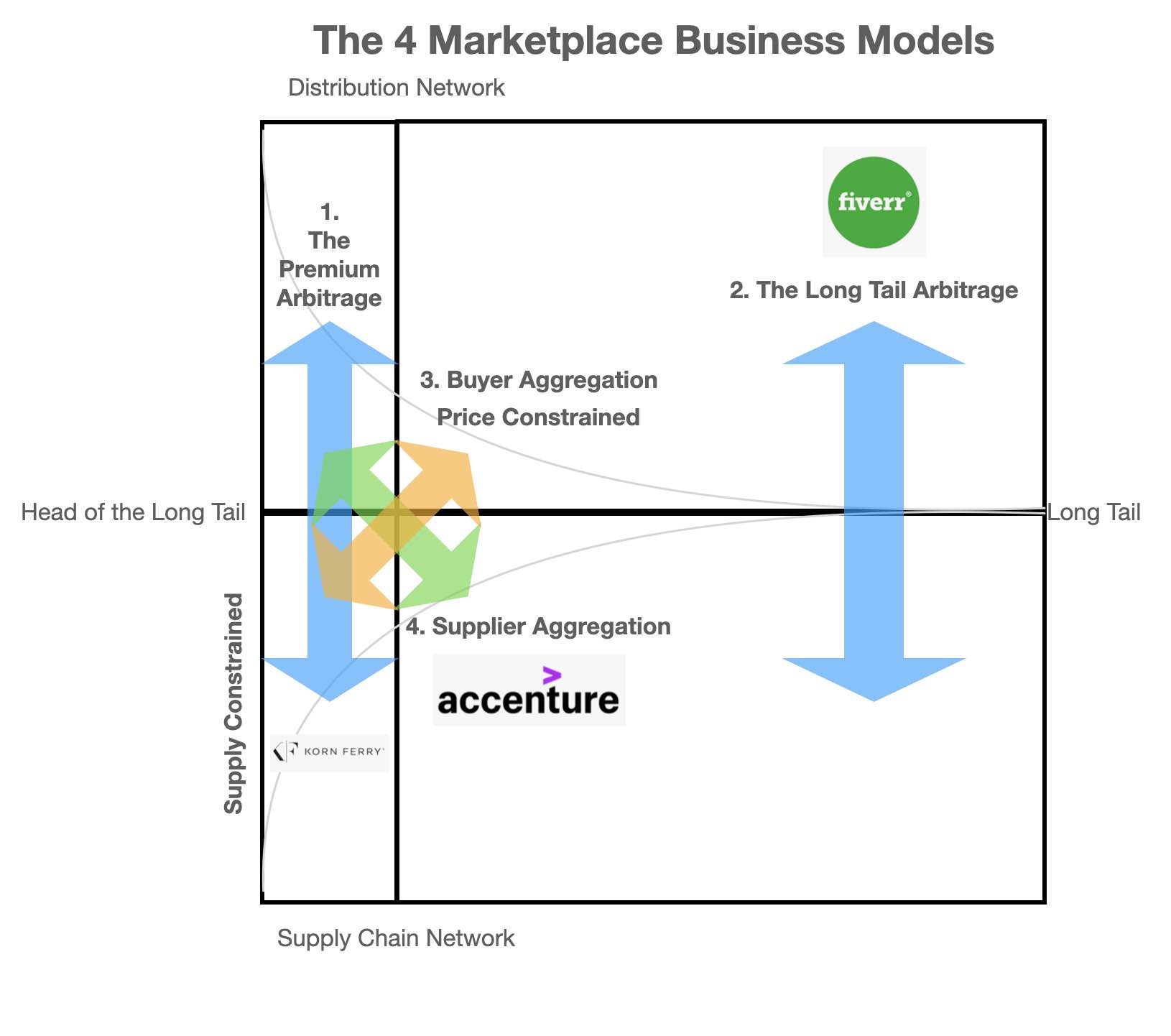
... and to make it even easier to understand let's add a few logos to the matrix
In this case the market leaders in the travel booking market
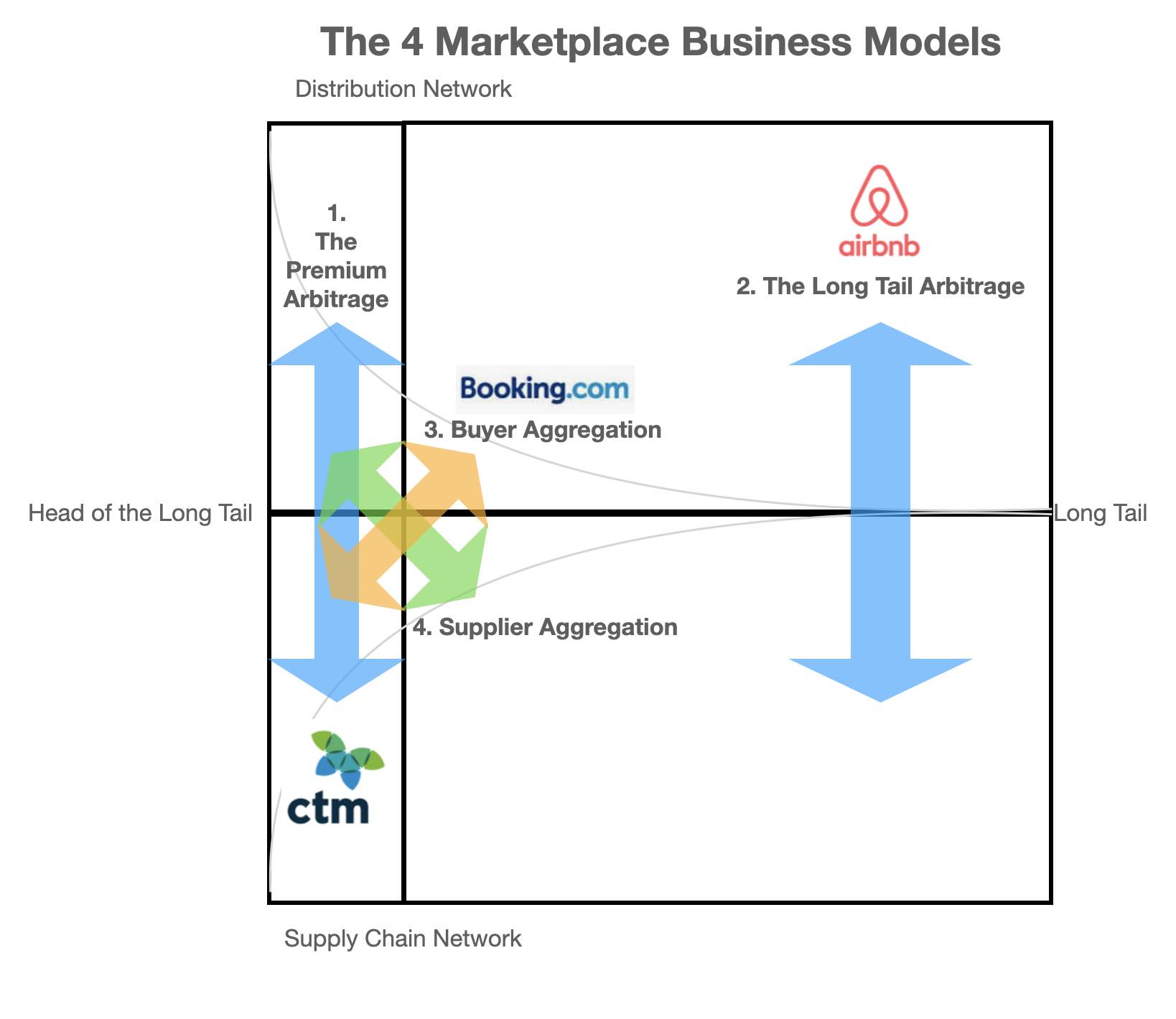
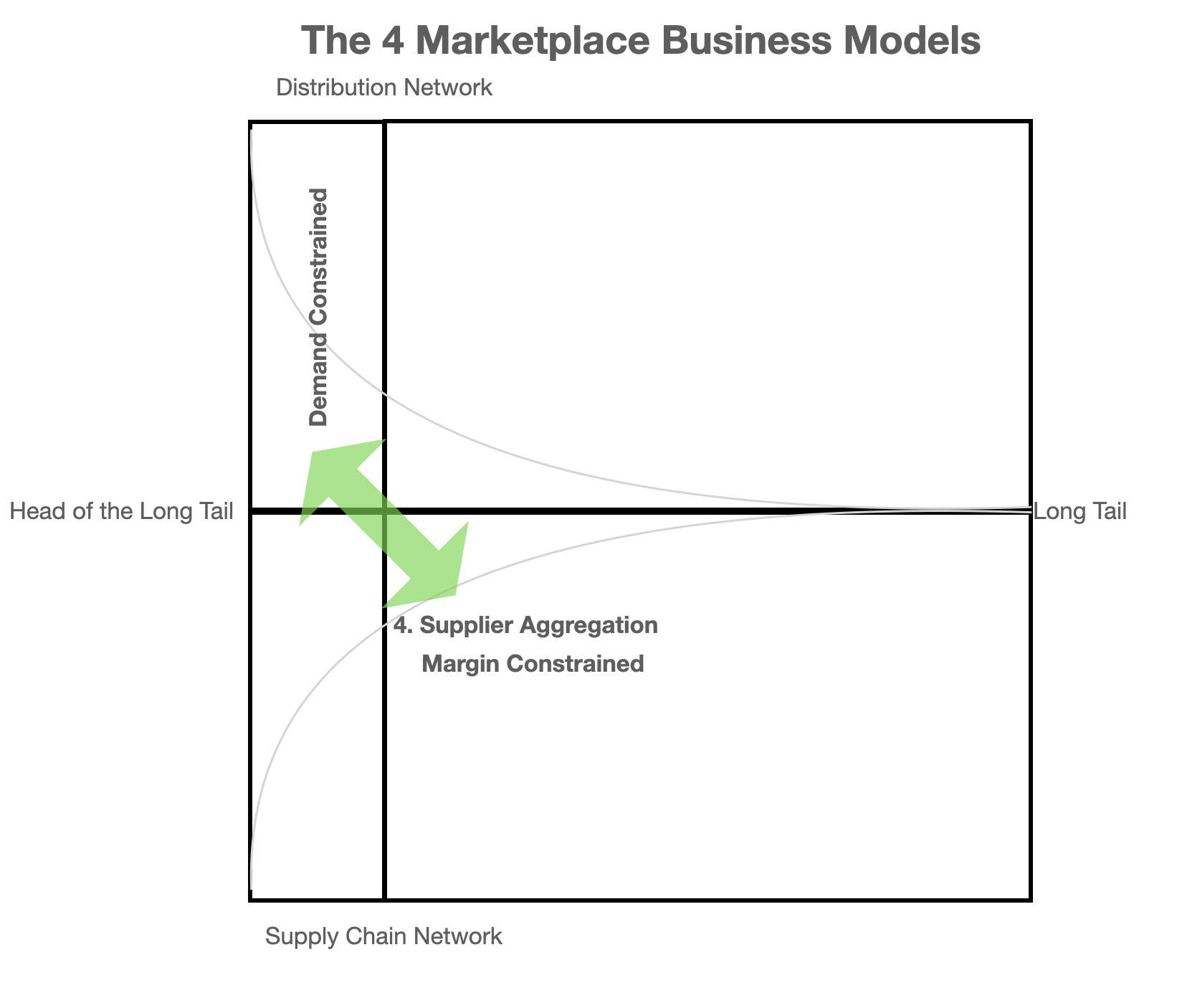
You'll note that I have left business model 4 vacant to demonstrate how some models are more difficult to build and scale than others (I'll explain why shortly)
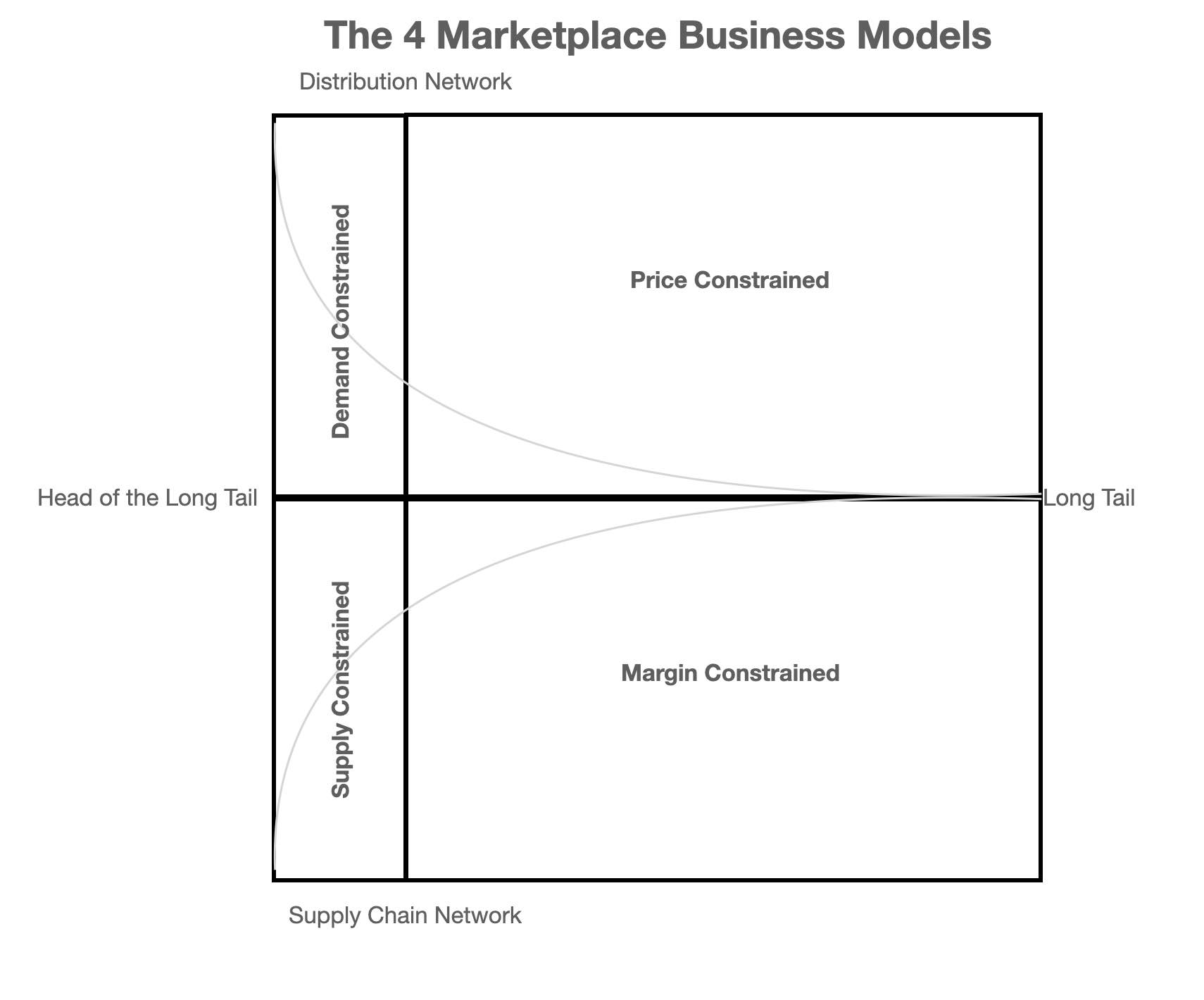
Moving on we can now examine the unique barriers to entry and scale for each of the four models
In the case of the Premium Arbitrage its both Demand and Supply Constraints
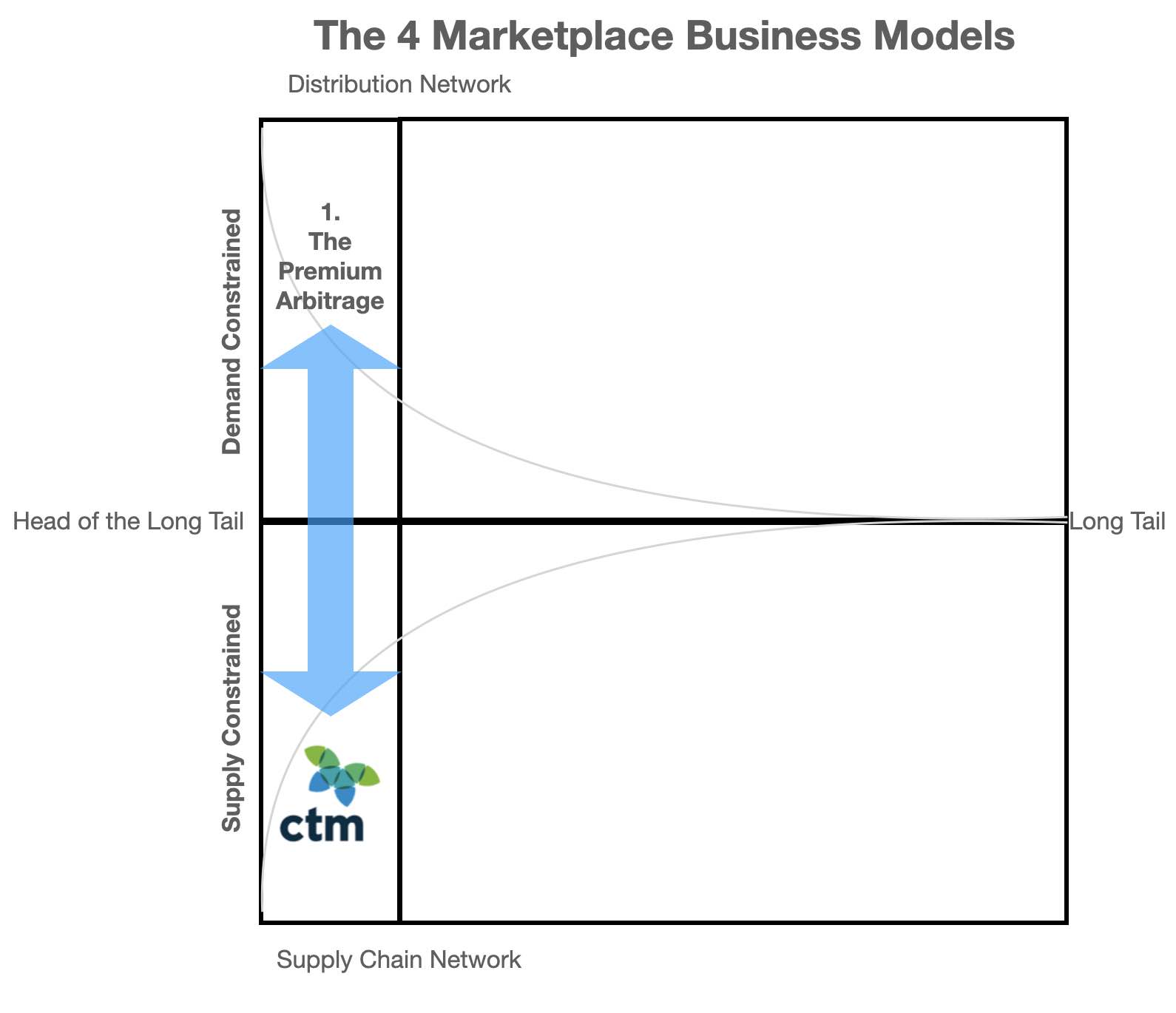
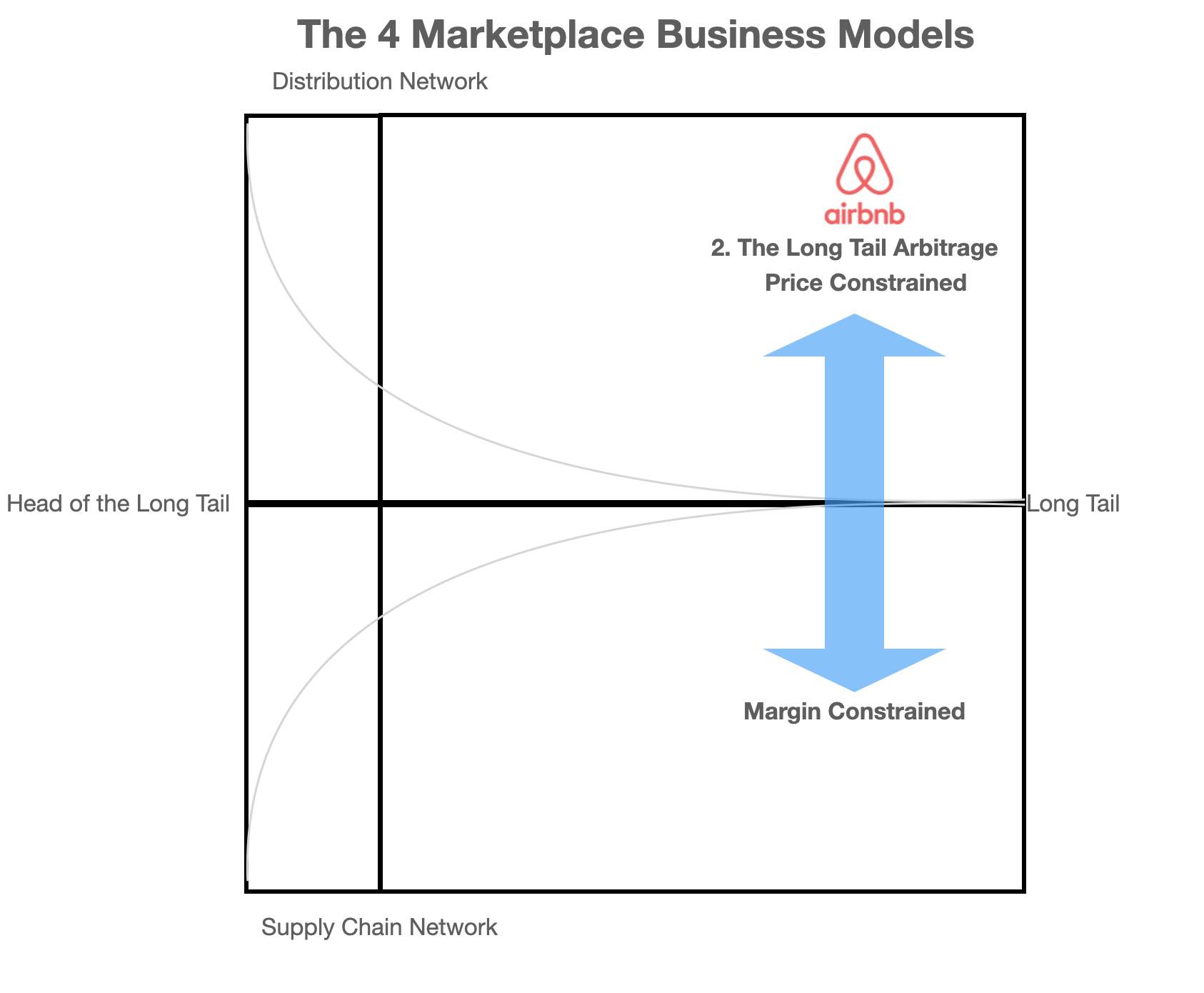
The AirBnB model suffers from Price and Margin Constraints
Note: There are quality issues on both the Demand and Supply side of aggregating the long tail. But we will put those aside for the moment
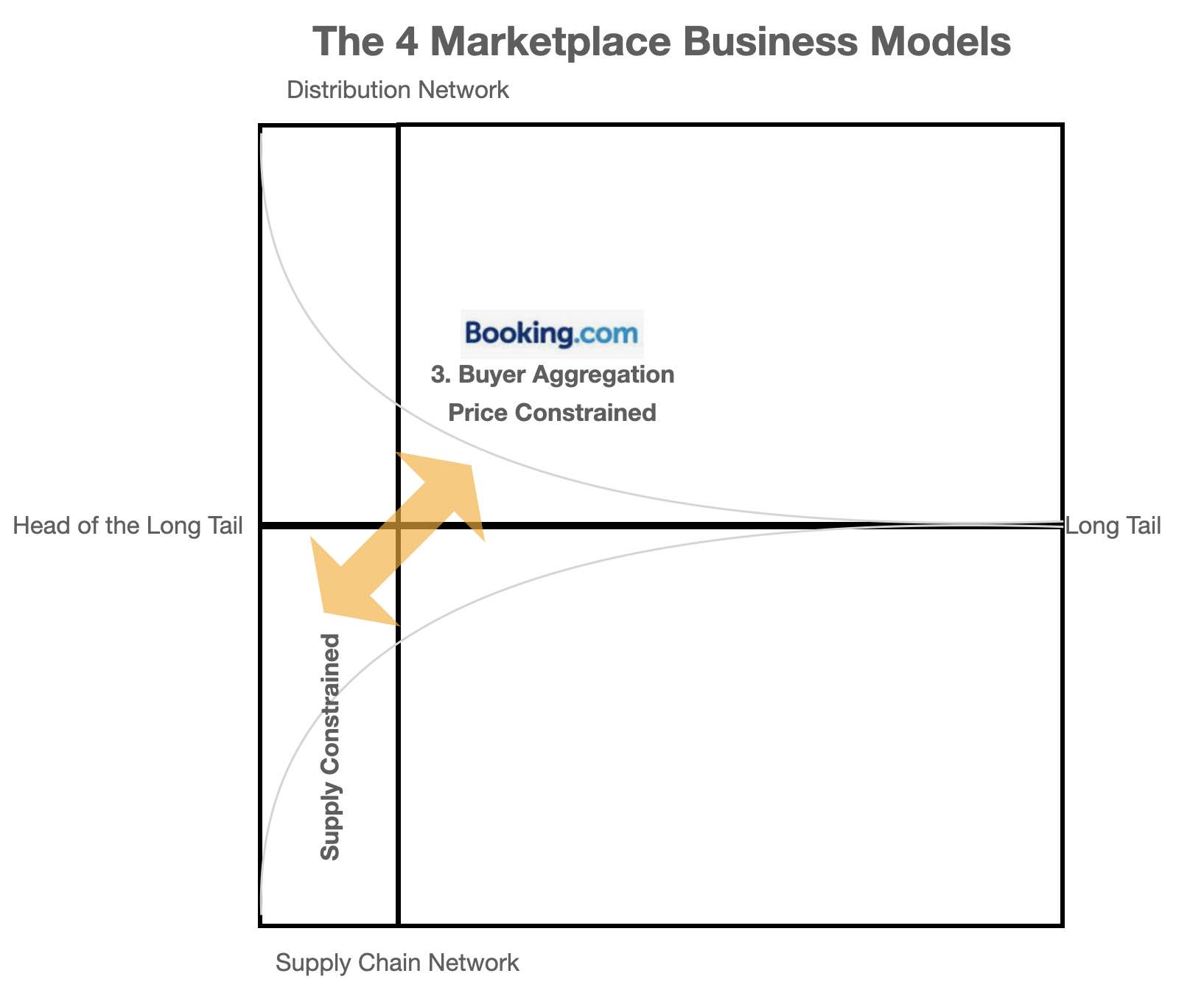
The Bookings.Com model suffers from Price and Supply Constraints
The fourth model suffers from Demand and Margin Constraints
and ultimately the ability of the premium model to modify its supply chain to leverage its market position to reduce its supply constraints
But this challenge isn't universal
We can see how it is Model 3 that is challenged in the HR market
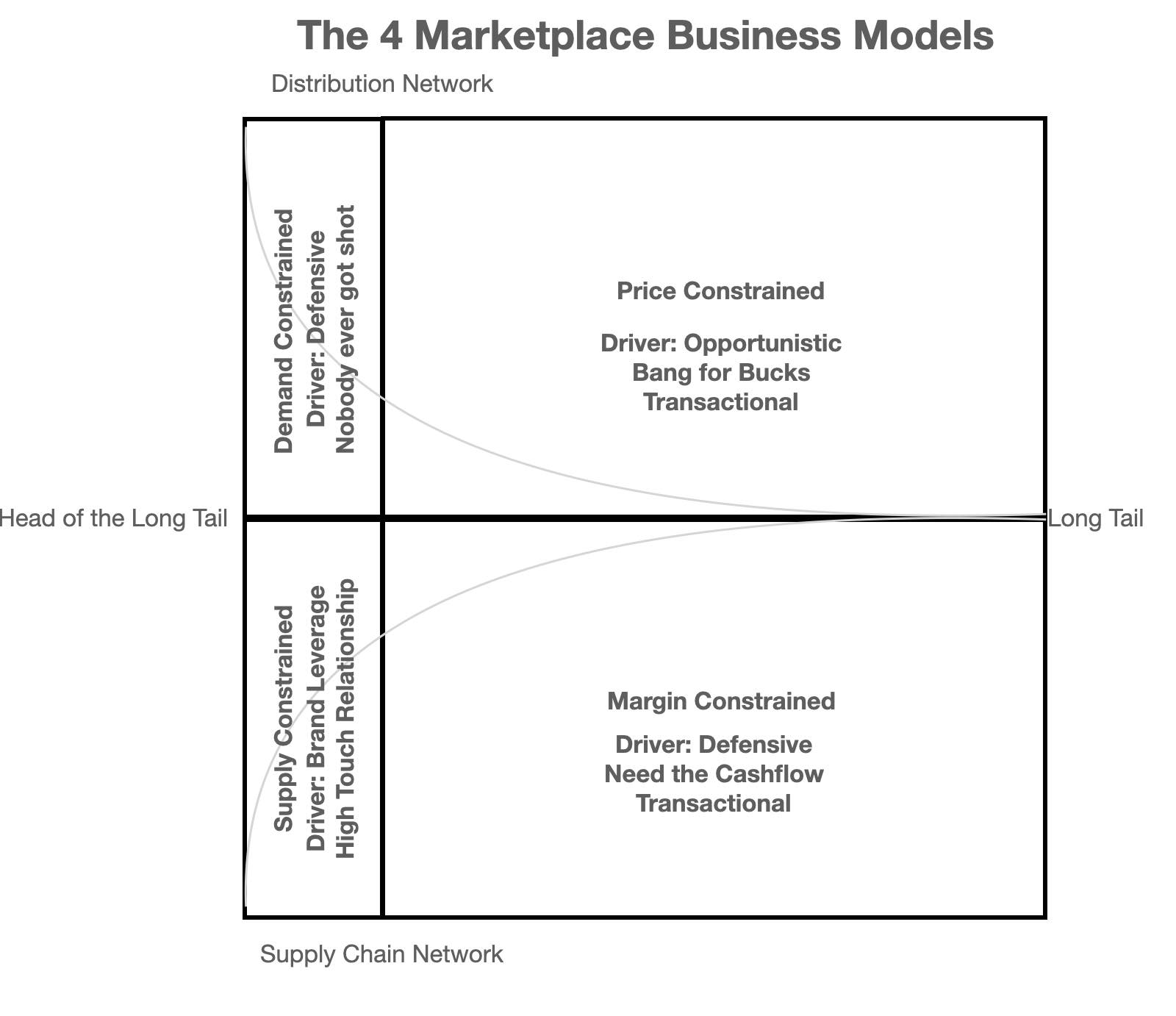
and if we apply the drivers we can see why this disconnect between the head and the tail is easy to delineate
Crossovers are hard because it is the chasm between having a strategic partnership and a transactional relationship
Closing thoughts?
These days it is redundant to suggest 2 Sided marketplaces are difficult to ignite and scale
Bringing buyers and sellers to the table is hard
The challenge, as I have stated elsewhere, is all about changing the story so you can change the game
Digital is obviously much easier to ignite and scale than physical simply because you can fake traffic and you can fake inventory
You'll notice I haven't mentioned networks effects - other than the above reference to machine generated traffic and inventory
This is because marketplaces are the aggregate sum of their arbitrages rather than the sum of their connections
The equation is Find Me, Find You and Let's Exchange
and is better understood as more of a 4-D state of flux than a static 2-D network of nodes and connections
Marketplaces win market share because they can deliver that just in time exchange on demand between parties who may never meet or choose to exchange again
Rendering the search for connections redundant
... and I'll leave you to think about that..
At least until next time...